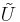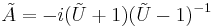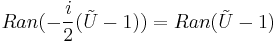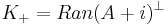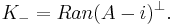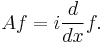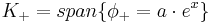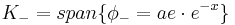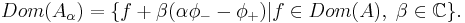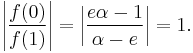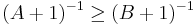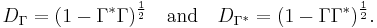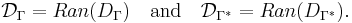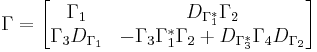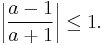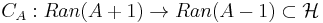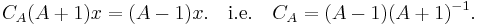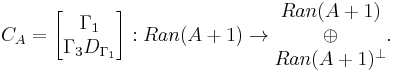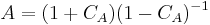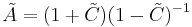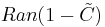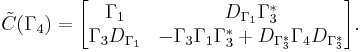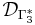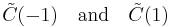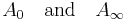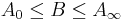Extensions of symmetric operators

In functional analysis, one is interested in extensions of symmetric operators acting on a Hilbert space. Of particular importance is the existence, and sometimes explicit constructions, of self-adjoint extensions. This problem arises, for example, when one needs to specify domains of self-adjointness for formal expressions of observables in quantum mechanics. Other applications of solutions to this problem can be seen in various moment problems.

This article discusses a few related problems of this type. The unifying theme is that each problem has an operator-theoretic characterization which gives a corresponding parametrization of solutions. More specifically, finding self-adjoint extensions, with various requirements, of symmetric operators is equivalent to finding unitary extensions of suitable partial isometries.

1 Symmetric operators
2 Extensions of symmetric operators
- 2.1 An example
3 Self adjoint extension on a larger space
4 Positive symmetric operators
- 4.1 Structure of 2 × 2 matrix contractions
- 4.2 Extensions of Positive symmetric operators
5 References

Symmetric operators

Let H be a Hilbert space. A linear operator A acting on H with dense domain Dom(A) is symmetric if

<Ax, y> = <x, Ay>, for all x, y in Dom(A).

If Dom(A) = H, the Hellinger-Toeplitz theorem says that A is a bounded operator, in which case A is self-adjoint and the extension problem is trivial. In general, a symmetric operator is self-adjoint if the domain of its adjoint, Dom(A*), lies in Dom(A).

When dealing with unbounded operators, it is often desirable to be able to assume that the operator in question is closed. In the present context, it is a convenient fact that every symmetric operator A is closable. That is, A has a smallest closed extension, called the closure of A. This can be shown by invoking the symmetric assumption and Riesz representation theorem. Since A and its closure have the same closed extensions, it can always be assumed that the symmetric operator of interest is closed.

In the sequel, a symmetric operator will be assumed to be densely defined and closed.

Extensions of symmetric operators

Problem Given a densely defined closed symmetric operator A, find its self-adjoint extensions.

This question can be translated to an operator-theoretic one. As a heuristic motivation, notice that the Cayley transform on the complex plane, defined by

$z \mapsto \frac{z-i}{z%2Bi}$

maps the real line to the unit circle. This suggests one define, for a symmetric operator A,

$U_A = (A - i)(A %2B i)^{-1}\,$

on Ran(A + i), the range of A + i. The operator U_A is in fact an isometry between closed subspaces that takes (A + i)x to (A - i)x for x in Dom(A). The map

$A \mapsto U_A$

is also called the Cayley transform of the symmetric operator A. Given U_A, A can be recovered by

$A = - i(U %2B 1)(U - 1)^{-1} ,\,$

defined on Dom(A) = Ran(U - 1). Now if

$\tilde{U}$

is an isometric extension of U_A, the operator

$\tilde{A} = - i( \tilde{U} %2B 1)( \tilde{U} - 1 )^{-1}$

acting on

$Ran (- \frac{i}{2} ( \tilde{U} - 1)) = Ran ( \tilde{U} - 1)$

is a symmetric extension of A.

Theorem The symmetric extensions of a closed symmetric operator A is in one-to-one correspondence with the isometric extensions of its Cayley transform U_A.

Of more interest is the existence of self-adjoint extensions. The following is true.

Theorem A closed symmetric operator A is self-adjoint if and only if Ran (A ± i) = H, i.e. when its Cayley transform U_A is a unitary operator on H.

Corollary The self-adjoint extensions of a closed symmetric operator A is in one-to-one correspondence with the unitary extensions of its Cayley transform U_A.

Define the deficiency subspaces of A by

$K_%2B = Ran(A%2Bi)^{\perp}$

and

$K_- = Ran(A-i)^{\perp}.$

In this language, the description of the self-adjoint extension problem given by the corollary can be restated as follows: a symmetric operator A has self-adjoint extensions if and only if its Cayley transform U_A has unitary extensions to H, i.e. the deficiency subspaces K₊ and K_- have the same dimension.

An example

Consider the Hilbert space L²[0,1]. On the subspace of absolutely continuous function that vanish on the boundary, define the operator A by

$A f = i \frac{d}{dx} f.$

Integration by parts shows A is symmetric. Its adjoint A* is the same operator with Dom(A*) being the absolutely continuous functions with no boundary condition. We will see that extending A amounts to modifying the boundary conditions, thereby enlarging Dom(A) and reducing Dom(A*), until the two coincide.

Direct calculation shows that K₊ and K_- are one dimensional subspaces given by

$K_%2B = span \{\phi_%2B = a \cdot e^x \}$

and

$K_- = span\{ \phi_- = ae \cdot e^{-x} \}$

where a is a normalizing constant. So the self-adjoint extensions of A are parametrized by the unit circle in the complex plane, {|α| = 1}. For each unitary U_α : K_- → K₊, defined by U_α(φ_-) = αφ₊, there corresponds an extension A_α with domain

$Dom(A_{\alpha}) = \{ f %2B \beta (\alpha \phi_{-} - \phi_%2B) | f \in Dom(A) , \; \beta \in \mathbb{C} \}.$

If f ∈ Dom(A_α), then f is absolutely continuous and

$\left|\frac{f(0)}{f(1)}\right| = \left|\frac{e\alpha -1}{\alpha - e}\right| = 1.$

Conversely, if f is absolutely continuous and f(0) = γf(1) for some complex γ with |γ| = 1, then f lies in the above domain.

The self-adjoint operators { A_α } are instances of the momentum operator in quantum mechanics.

Self adjoint extension on a larger space

Every partial isometry can be extended, on a possibly larger space, to a unitary operator. Consequently, every symmetric operator has a self-adjoint extension, on a possibly larger space.

Positive symmetric operators

A symmetric operator A is called positive if <Ax, x> ≥ 0 for all x in Dom(A). It is known that for every such A, one has dim(K₊) = dim(K_-). Therefore every positive symmetric operator has self-adjoint extensions. The more interesting question in this direction is whether A has positive self-adjoint extensions.

For two positive operators A and B, we put A ≤ B if

$(A %2B 1)^{-1} \ge (B %2B 1)^{-1}$

in the sense of bounded operators.

Structure of 2 × 2 matrix contractions

While the extension problem for general symmetric operators is essentially that of extending partial isometries to unitaries, for positive symmetric operators the question becomes one of extending contractions: by "filling out" certain unknown entries of a 2 × 2 self-adjoint contraction, we obtain the positive self-adjoint extensions of a positive symmetric operator.

Before stating the relevant result, we first fix some terminology. For a contraction Γ, acting on H, we define its defect operators by

$D_{ \Gamma } = (1 - \Gamma^*\Gamma )^{\frac{1}{2}} \quad \mbox{and} \quad D_{\Gamma^*} = (1 - \Gamma \Gamma^*)^{\frac{1}{2}}.$

The defect spaces of Γ are

$\mathcal{D}_{\Gamma} = Ran( D_{\Gamma} ) \quad \mbox{and} \quad \mathcal{D}_{\Gamma^*} = Ran( D_{\Gamma^*} ).$

The defect operators indicate the non-unitarity of Γ, while the defect spaces ensure uniqueness in some parameterizations. Using this machinery, one can explicitly describe the structure of general matrix contractions. We will only need the 2 × 2 case. Every 2 × 2 contraction Γ can be uniquely expressed as

$\Gamma = \begin{bmatrix} \Gamma_1 & D_{\Gamma_1 ^*} \Gamma_2\\ \Gamma_3 D_{\Gamma_1} & - \Gamma_3 \Gamma_1^* \Gamma_2 %2B D_{\Gamma_3 ^*} \Gamma_4 D_{\Gamma_2} \end{bmatrix}$

where each Γ_i is a contraction.

Extensions of Positive symmetric operators

The Cayley transform for general symmetric operators can be adapted to this special case. For every non-negative number a,

$\left|\frac{a-1}{a%2B1}\right| \le 1.$

This suggests we assign to every positive symmetric operator A a contraction

$C_A�: Ran(A %2B 1) \rightarrow Ran(A-1) \subset \mathcal{H}$

defined by

$C_A (A%2B1)x = (A-1)x. \quad \mbox{i.e.} \quad C_A = (A-1)(A%2B1)^{-1}.\,$

which have matrix representation

$C_A = \begin{bmatrix} \Gamma_1 \\ \Gamma_3 D_{\Gamma_1} \end{bmatrix} : Ran(A%2B1) \rightarrow \begin{matrix} Ran(A%2B1) \\ \oplus \\ Ran(A%2B1)^{\perp} \end{matrix}.$

It is easily verified that the Γ₁ entry, C_A projected onto Ran(A + 1) = Dom(C_A), is self-adjoint. The operator A can be written as

$A = (1%2B C_A)(1 - C_A)^{-1} \,$

with Dom(A) = Ran(C_A - 1). If

$\tilde{C}$

is a contraction that extends C_A and its projection onto its domain is self-adjoint, then it is clear that its inverse Cayley transform

$\tilde{A} = ( 1 %2B \tilde{C} ) ( 1 - \tilde{C} )^{-1}$

defined on

$Ran ( 1 - \tilde{C} )$

is a positive symmetric extension of A. The symmetric property follows from its projection onto its own domain being self-adjoint and positivity follows from contractivity. The converse is also true: given a positive symmetric extension of A, its Cayley transform is a contraction satisfying the stated "partial" self-adjoint property.

Theorem The positive symmetric extensions of A are in one-to-one correspondence with the extensions of its Cayley transform where if C is such an extension, we require C projected onto Dom(C) be self-adjoint.

The unitarity criterion of the Cayley transform is replaced by self-adjointness for positive operators.

Theorem A symmetric positive operator A is self-adjoint if and only if its Cayley transform is a self-adjoint contraction defined on all of H, i.e. when Ran(A + 1) = H.

Therefore finding self-adjoint extension for a positive symmetric operator becomes a matrix "completion problem". Specifically, we need to embed the column contraction C_A into a 2 × 2 self-adjoint contraction. This can always be done and the structure of such contractions gives a parametrization of all possible extensions.

By the preceding subsection, all self-adjoint extensions of C_A takes the form

$\tilde{C}(\Gamma_4) = \begin{bmatrix} \Gamma_1 & D_{\Gamma_1} \Gamma_3 ^* \\ \Gamma_3 D_{\Gamma_1} & - \Gamma_3 \Gamma_1 \Gamma_3^* %2B D_{\Gamma_3^*} \Gamma_4 D_{\Gamma_3^*} \end{bmatrix}.$

So the self-adjoint positive extensions of A are in bijective correspondence with the self-adjoint contractions Γ₄ on the defect space

$\mathcal{D}_{\Gamma_3^*}$

of Γ₃. The contractions

$\tilde{C}(-1) \quad \mbox{and} \quad \tilde{C}(1)$

give rise to positive extensions

$A_0 \quad \mbox{and} \quad A_{\infty}$

respectively. These are the smallest and largest positive extensions of A in the sense that

$A_0 \leq B \leq A_{\infty}$

for any positive self-adjoint extension B of A. The operator A_∞ is the Friedrichs extension of A and A₀ is the von Neumann-Krein extension of A.

Similar results can be obtained for accretive operators.

References

A. Alonso and B. Simon, The Birman-Krein-Vishik theory of self-adjoint extensions of semibounded operators. J. Operator Theory 4 (1980), 251-270.

Gr. Arsene and A. Gheondea, Completing matrix contractions, J. Operator Theory 7 (1982), 179-189.

N. Dunford and J.T. Schwartz, Linear Operators, Part II, Interscience, 1958.

M. Reed and B. Simon, Methods of Modern Mathematical Physics, vol. I and II, Academic Press, 1975.

Extensions of symmetric operators

Contents

Symmetric operators

Extensions of symmetric operators

An example

Self adjoint extension on a larger space

Positive symmetric operators

Structure of 2 × 2 matrix contractions

Extensions of Positive symmetric operators

References